Recently there was a suggestion posted to the Beginner’s PID Series. The contention was that if you solve things in the Laplace domain, it specifies a different way of executing the Integral Term. Rather than looking at the sum of error for THIS point, the commenter suggested, you should look at the sum from the last point.
So the current code is this:
/*Compute all the working error variables*/
double input = *myInput;
double error = *mySetpoint - input;
ITerm+= (ki * error);
if(ITerm > outMax) ITerm= outMax;
else if(ITerm < outMin) ITerm= outMin;
double dInput = (input - lastInput);
/*Compute PID Output*/
double output = kp * error + ITerm- kd * dInput;
and the suggestion was this:
/*Compute all the working error variables*/
double input = *myInput;
double error = *mySetpoint - input;
double dInput = (input - lastInput);
/*Compute PID Output*/
double output = kp * error + ITerm- kd * dInput;
ITerm+= (ki * error);
if(ITerm > outMax) ITerm= outMax;
else if(ITerm < outMin) ITerm= outMin;
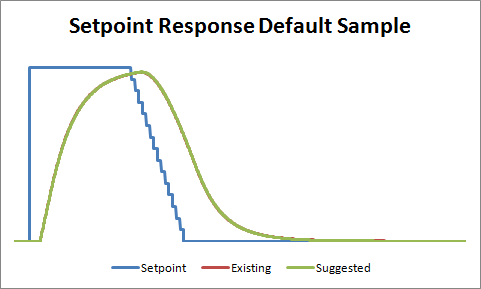
I had never seen it done this way, but I figured I’d give it a shot. The test I devised was a simple setpoint step, followed by a ramp down.
With the controller set at the default sample time, the difference was imperceptible. To try and highlight the difference between the two methods, I decided to bump up the PID sample time from the default of 100mS to 5 seconds.
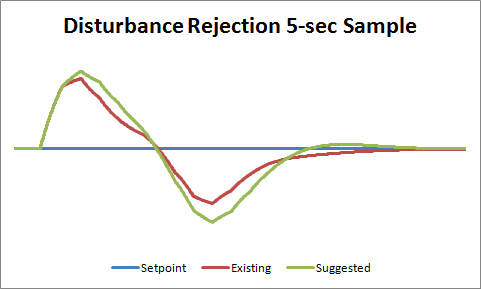
Ok so here we can see a clear winner. The existing PID code performs better than suggested, probably because the integral term gets to react to process changes 5 seconds sooner. But just to make sure I wasn’t missing anything, I decided to do another test. Instead of a setpoint change, I induced a load change in the system.
Once again, the existing PID code performed better, handling the load change more quickly.
So the verdict? While this was a fun excersize, I think the results are clear. I’ll leave the code as it is.





Thanks for taking the time to compare! I check the math and find out that I was using an aproximation for my PID. That aproximation is not needed here (it’s more for n degree sofware filtering).
As this post is more than a year old, I don’t know if this is the best way to tell this. In case you think there’s a better place to send it, please let me know.
In fact, the quantification error produced by both approximations (the one implemented by @Brett and the change @jojo proposed) is nearly the same.
When solving in the Laplace domain, the transfer function of the integral term is Ki/s. The Laplace domain is meant for continuous time, though, so any digital implementation (discrete) will produce not exact measurements. There is another domain, called Z, which is meant for discrete time. So, when implementing transfer functions in digital systems, we should take this as a reference.
When changing from the Laplace domain to the Z domain, we can use three different transformations: Euler’s Fordward Difference (@jojo), Backward Difference (@Brett) and Tustin’s or Bilinear. Attending to the meaning of integration, which is calculating the
area below a function, we can analyze those three different approaches graphically:
https://ia601207.us.archive.org/28/items/IntegralTermComparison/intcomp.png
As you can see, both the Fordward and Backward approaches take the area as a rectangle. The first one, takes the previous sample and pushes it fordward, assuming the signal is constant from (k-1)Ts to kTs (Ts=sampling period). The second one makes the same, but taking the last sample as constant value, so pushing it backward. In fact, the performance of both of them should be the same. Although when changing the setpoint to a greater value the Backward method is faster (because it quantifies more than the ideal integration), when setting it to a lower one they sweep. So, depending on the application, especially in bipolar ones (i.e. controlling a motor in two directions), we’ll get no better performance with none of them.
The third approach, Tustin’s, takes the area as a trapezoid, considerably reducing the quantification error and getting a value just in the middle between the previous ones. So attending to theory, this would be the best one (there are also mathematical reasons I don’t get to understand which say so).
When talking about implementation, you can see that this approach needs adding the last and the previous error samples. The division can be done to Ki, the same way you did with Ts, so its value will be 1 bit smaller, which will compensate that the other operand is 1 bit larger. As you don’t save lastError value, this (my) suggestion has two instructions more than your actual design, and changes just other two lines:
double iInput = (error + lastError);
ITerm+= (ki * iInput);
lastError = error;
…
ki = Ki * SampleTimeInSec / 2;
—————————–
Apart from that suggestion, when you performed the comparison with Ts=5s, the systems were probably not meeting the plant timing requirements, which means the controller’s work speed was not enough for a good performance. Although it can be used, depending on the application, not having into account the plant dynamics can lead to unstable responses. For an optimal control system we should try to meet the Real Time requirements (which typically means to set the sample time at least 10 times lower than the minimum change time in the plant).
In the setpoint response comparison, when starting the ramp down, the existing system has reached its steady-state value (nearly the setpoint value), while the system suggested by @jojo is still transitory. For a better analysis I think it would be good to wait until both systems have reached their steady-state value, before changing the setpoint.
In the disturbance rejection comparison we can see that the existing one (@Brett, Backward) performs better with positive disturbances, but the suggested one (@jojo, Fordward) is quite faster with negatives (besides initial states not being the same), es exposed previously.
Finally, I hope you can excuse me for my bad english, and I wish this information/explanation will help you improve this great library. I would also like to congratulate you not only for doing it, but for writing all these explanations to help beginners understand easily control.
Opositivo