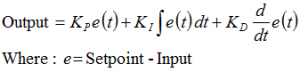(This is Modification #1 in a larger series on writing a solid PID algorithm)
The Problem
The Beginner’s PID is designed to be called irregularly. This causes 2 issues:
- You don’t get consistent behavior from the PID, since sometimes it’s called frequently and sometimes it’s not.
- You need to do extra math computing the derivative and integral, since they’re both dependent on the change in time.
The Solution
Ensure that the PID is called at a regular interval. The way I’ve decided to do this is to specify that the compute function get called every cycle. based on a pre-determined Sample Time, the PID decides if it should compute or return immediately.
Once we know that the PID is being evaluated at a constant interval, the derivative and integral calculations can also be simplified. Bonus!
The Code
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
errSum += error;
double dErr = (error - lastErr);
/*Compute PID Output*/
Output = kp * error + ki * errSum + kd * dErr;
/*Remember some variables for next time*/
lastErr = error;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
On lines 10&11, the algorithm now decides for itself if it’s time to calculate. Also, because we now KNOW that it’s going to be the same time between samples, we don’t need to constantly multiply by time change. We can merely adjust the Ki and Kd appropriately (lines 31 & 32) and result is mathematically equivalent, but more efficient.
one little wrinkle with doing it this way though though. if the user decides to change the sample time during operation, the Ki and Kd will need to be re-tweaked to reflect this new change. that’s what lines 39-42 are all about.
Also Note that I convert the sample time to Seconds on line 29. Strictly speaking this isn’t necessary, but allows the user to enter Ki and Kd in units of 1/sec and s, rather than 1/mS and mS.
The Results
the changes above do 3 things for us
- Regardless of how frequently Compute() is called, the PID algorithm will be evaluated at a regular interval [Line 11]
- Because of the time subtraction [Line 10] there will be no issues when millis() wraps back to 0. That only happens every 55 days, but we’re going for bulletproof remember?
- We don’t need to multiply and divide by the timechange anymore. Since it’s a constant we’re able to move it from the compute code [lines 15+16] and lump it in with the tuning constants [lines 31+32]. Mathematically it works out the same, but it saves a multiplication and a division every time the PID is evaluated
Side note about interrupts
If this PID is going into a microcontroller, a very good argument can be made for using an interrupt. SetSampleTime sets the interrupt frequency, then Compute gets called when it’s time. There would be no need, in that case, for lines 9-12, 23, and 24. If you plan on doing this with your PID implentation, go for it! Keep reading this series though. You’ll hopefully still get some benefit from the modifications that follow.
There are three reasons I didn’t use interrupts
- As far as this series is concerned, not everyone will be able to use interrupts.
- Things would get tricky if you wanted it implement many PID controllers at the same time.
- If I’m honest, it didn’t occur to me. Jimmie Rodgers suggested it while proof-reading the series for me. I may decide to use interrupts in future versions of the PID library.