(This is Modification #4 in a larger series on writing a solid PID algorithm)
The Problem

Reset windup is a trap that probably claims more beginners than any other. It occurs when the PID thinks it can do something that it can’t. For example, the PWM output on an Arduino accepts values from 0-255. By default the PID doesn’t know this. If it thinks that 300-400-500 will work, it’s going to try those values expecting to get what it needs. Since in reality the value is clamped at 255 it’s just going to keep trying higher and higher numbers without getting anywhere.
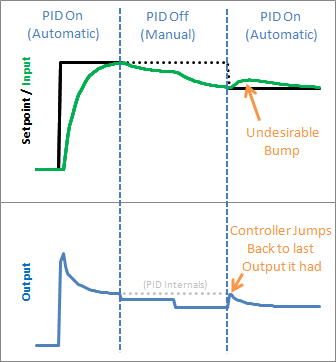
The problem reveals itself in the form of weird lags. Above we can see that the output gets “wound up” WAY above the external limit. When the setpoint is dropped the output has to wind down before getting below that 255-line.
The Solution – Step 1

There are several ways that windup can be mitigated, but the one that I chose was as follows: tell the PID what the output limits are. In the code below you’ll see there’s now a SetOuputLimits function. Once either limit is reached, the pid stops summing (integrating.) It knows there’s nothing to be done; Since the output doesn’t wind-up, we get an immediate response when the setpoint drops into a range where we can do something.
The Solution – Step 2
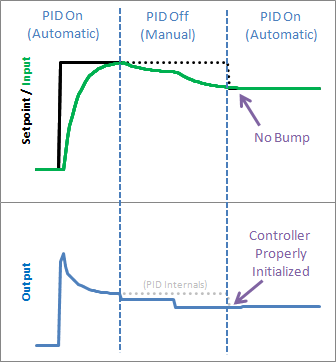
Notice in the graph above though, that while we got rid that windup lag, we’re not all the way there. There’s still a difference between what the pid thinks it’s sending, and what’s being sent. Why? the Proportional Term and (to a lesser extent) the Derivative Term.
Even though the Integral Term has been safely clamped, P and D are still adding their two cents, yielding a result higher than the output limit. To my mind this is unacceptable. If the user calls a function called “SetOutputLimits” they’ve got to assume that that means “the output will stay within these values.” So for Step 2, we make that a valid assumption. In addition to clamping the I-Term, we clamp the Output value so that it stays where we’d expect it.
(Note: You might ask why we need to clamp both. If we’re going to do the output anyway, why clamp the Integral separately? If all we did was clamp the output, the Integral term would go back to growing and growing. Though the output would look nice during the step up, we’d see that telltale lag on the step down.)
The Code
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
ITerm+= (ki * error);
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ITerm- kd * dInput;
if(Output > outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
void SetOutputLimits(double Min, double Max)
{
if(Min > Max) return;
outMin = Min;
outMax = Max;
if(Output > outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
}
A new function was added to allow the user to specify the output limits [lines 52-63]. And these limits are used to clamp both the I-Term [17-18] and the Output [23-24]
The Result
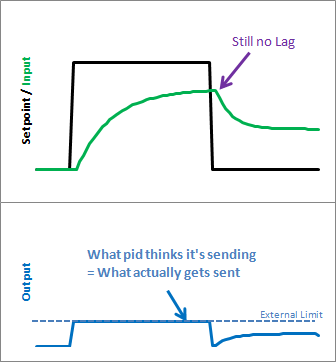
As we can see, windup is eliminated. in addition, the output stays where we want it to. this means there’s no need for external clamping of the output. if you want it to range from 23 to 167, you can set those as the Output Limits.
Next >>