Recently there was a suggestion posted to the Beginner’s PID Series. The contention was that if you solve things in the Laplace domain, it specifies a different way of executing the Integral Term. Rather than looking at the sum of error for THIS point, the commenter suggested, you should look at the sum from the last point.
So the current code is this:
/*Compute all the working error variables*/
double input = *myInput;
double error = *mySetpoint - input;
ITerm+= (ki * error);
if(ITerm > outMax) ITerm= outMax;
else if(ITerm < outMin) ITerm= outMin;
double dInput = (input - lastInput);
/*Compute PID Output*/
double output = kp * error + ITerm- kd * dInput;
and the suggestion was this:
/*Compute all the working error variables*/
double input = *myInput;
double error = *mySetpoint - input;
double dInput = (input - lastInput);
/*Compute PID Output*/
double output = kp * error + ITerm- kd * dInput;
ITerm+= (ki * error);
if(ITerm > outMax) ITerm= outMax;
else if(ITerm < outMin) ITerm= outMin;
I had never seen it done this way, but I figured I’d give it a shot. The test I devised was a simple setpoint step, followed by a ramp down.
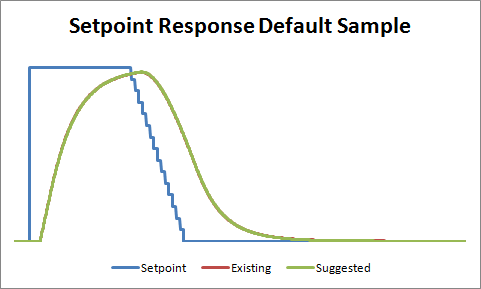
With the controller set at the default sample time, the difference was imperceptible. To try and highlight the difference between the two methods, I decided to bump up the PID sample time from the default of 100mS to 5 seconds.

Ok so here we can see a clear winner. The existing PID code performs better than suggested, probably because the integral term gets to react to process changes 5 seconds sooner. But just to make sure I wasn’t missing anything, I decided to do another test. Instead of a setpoint change, I induced a load change in the system.
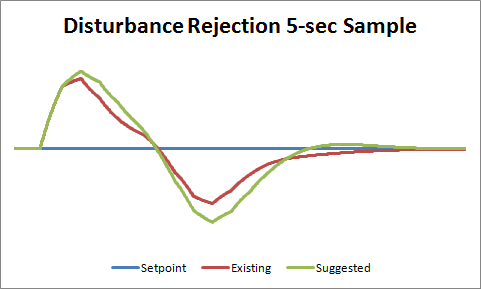
Once again, the existing PID code performed better, handling the load change more quickly.
So the verdict? While this was a fun excersize, I think the results are clear. I’ll leave the code as it is.